Optimizing the Stalemate: Limited Conflicts and the Use of Special Operations Forces in the Context of Global Competition

Introduction

The ignominious end of the war in Afghanistan raises many questions about what could have been accomplished there and, more importantly, what the future holds for the efficacy of limited armed conflict as a viable instrument for great powers.[i] The disastrous nature of the American withdrawal, however, has overshadowed deeper debate concerning the purpose and sustainability of any future such conflicts. One month after the last troops departed Kabul International Airport, President Biden’s top generals publicly contradicted him, saying that they had recommended maintaining a reduced military force as opposed to complete withdrawal.[ii] What was not articulated by these military leaders, however, was any fresh thinking to optimally employ such a small military footprint. We offer one here. Though our prescriptive model comes too late to change the outcome of Afghanistan, it is relevant for any future asymmetric military conflicts engaged in by the United States. More specifically, our model of tacit collusion (a) provides specific prescriptions for sustaining and managing limited armed conflict within the context of global competition, and (b) provides a scalable logic that can be extended to other domains of global competition. In brief, we examine conflicts in which neither side can defeat the other and bargained settlements are not possible. Our model shows that actors in such conflicts can arrive at an equilibrium where they refrain from wasteful fighting, but rather identify a mutually acceptable state of affairs in which each actor uses limited applications of pain to maintain the equilibrium. It is even possible to identify additional points of shared interest among warring actors around which limited cooperation may be fostered.

This model is designed to provide novel strategic concepts for “unwinnable” conflicts–when victory is not possible, and resources are limited. Beyond stalemated armed conflicts, our model also seeks to provide a logical basis for grounding the emerging doctrinal concept of “strategic competition,” which is defined by the Joint Chiefs of Staff as “an enduring condition to be managed, not a problem to be solved.”[iii] Further, our model has significant implications for U.S. Special Operations Forces (SOF). If our arguments have merit, then U.S. SOF forces would seem to be well-suited to engage in the types of activities suggested here. This is due to their ability to plan and conduct strategically oriented operations with a minimal footprint, as well as their pre-existing skillsets in irregular warfare and familiarity with politically sensitive activities. In sum, this model would provide a novel blueprint for U.S. SOF activities within a global competition environment.

To contextualize our model, let us consider why the United States chose to abandon the war in Afghanistan. By the last few years of the two-decades long conflict, critics often decried the war as a “stalemate,”[iv] with that term even becoming regularly used by U.S. military leadership.[v] This criticism even dominated the debate on Afghanistan in the 2020 presidential election as both candidates promised to end the war, due its stalemated condition.[vi] Donald Trump referred to the war as “ridiculously endless”[vii] and Biden referred to it as a “forever war.”[viii] In the words of one critic:

The trouble is that continuous war violates a core precept of strategy, which, at least as presently understood, involves the relation of means and ways to defined ends, not indefinite pursuits. If a campaign has no end, it can have no objective; if it has no objective, it cannot be won.[ix]

But do all conflicts need to be “won” for military activity to have purpose? If Clausewitz is correct in asserting that there is “a whole category of wars in which the very idea of defeating the enemy is unreal,” then can strategies be developed to pursue goals while eschewing traditional concepts of “winning?”[x]

Not only did Afghanistan appear to be “unwinnable,” but the enormous costs associated with the war began to be seen as a liability, as adversarial peer powers began to rise and the opportunity cost of pouring money into the Afghan stalemate began to elicit concern at the grand strategic level. How might the United States have optimized the war within this set of conditions? By drawing on the logic of tacit collusive models from oligopolistic competition among firms, we propose a reconceptualization of comparative strategies for managing such stalemated conflicts. To do so, we construct a model that escapes the constraints imposed by the pursuit of either military “victory” or a formal diplomatic conclusion. More specifically, we explore the possibility of identifying and fostering equilibria that are Pareto superior to continued active warfighting. The strategy to achieve such an outcome builds on the dynamics of oligopoly; how do rival firms engage in price fixing in the face of anti-trust laws? They use tacit mechanisms to arrive at mutually beneficial outcomes in which actors coordinate on equilibria without overt contracts with one another. In terms of military strategy, the advantage of such an approach is that it defines practicable goals in unwinnable conflicts, it logically nests tactical lines of effort underneath a well-defined strategic vision, and it entails relatively low costs and risks.

The paper proceeds as follows. First, we discuss the relevant literature on bargaining and war outcomes, and then focus particularly on the problematic aspects of internal wars. This provides a conceptual foundation upon which to build our treatment of asymmetric military interventions. We then discuss the use of the “Tulluck contest” as the most common framework currently chosen for the formal modeling of war termination and why it is inappropriate for our needs here (due to its supposition of clear a winner and loser in the modeled contest). We then proceed to construct and solve an alternative model based on oligopolistic competition; using such an approach allows us to provide the formal characterization of an equilibrium in which actors may optimally stabilize a conflict and even foster cooperation on other mutually desired outcomes despite neither being able to dominate the battlefield or engage in diplomatic bargaining. Finally, we return to the case of Afghanistan and counterfactually apply some of the model’s implications to that forsaken war.[xi]

Bargaining and War Outcomes: Unexplored Equilibria for Unwinnable Wars

To build our argument, we first review the application of bargaining models to the puzzle of war termination. We then narrow our discussion to the dynamics of war termination for intrastate conflicts. More specifically, we focus on this subset of conflicts to highlight four commonly observed aspects of internal wars that are also found in the population of protracted asymmetric military interventions that are relevant here.[xii] These four aspects are: the inability for either actor to achieve decisive military victory, inherent instabilities that hinder negotiated settlements, the frequent presence of “profitable” rent-streams that sustain the conflict, and the often fractured nature of the warring actors. After discussing each of these attributes in turn, we then set the stage for their employment in our model.

  The study of war termination has a relatively short and thin history. As late as 2009, Reiter could still lament that “[w]e know relatively little about how wars end, in contrast to the mountain ranges of ideas and scholarship we have about how wars start … war termination must receive closer attention.”[xiii] Kecskemeti and Ikle began the modern agenda on war termination by examining the strategic nature of surrender and how prewar visions of quick victory often diverge from the duration and costs of actual wars.[xiv] More recent efforts, such as Stam, Goemans, and Reiter build on the seminal work of Wittman and Pillar and emphasize war termination as a bargaining process.[xv] As actors fight one another the conflict may culminate in a total military victory in which one side is completely disarmed and left at the mercy of the other, but it is more likely to result in a diplomatic settlement somewhere short of total subjugation, with the exchange of violence serving as a form of bargaining that drives the terms of the settlement. This logic can be seen to reflect Clausewitz’s famous dictum that war is a continuation of politics and those political aims are often limited.[xvi] In typical analyses of inter-state war outcomes, wars can be decided militarily (either side wins through force of arms), or a “draw” can occur when “both sides are willing to accept [an] … outcome through some form of negotiated settlement.”[xvii] Within this framework fighting serves two purposes: it can reveal information about the likelihood of either side winning the war, and it can also serve to change that likelihood (by degrading the capabilities of the actors at varying rates).[xviii] In other words, a “military contest is like a very costly experiment that tests competing theories as to how the war will unfold.”[xix] Internal wars, however, often confound this characterization.

  First, is the inability of either side to achieve decisive military victory in the conflict. The inter-state war termination literature centers on the use of fighting to reveal information to the participants.[xx] As they fight, their expectations about outcomes become more consistent with one another, allowing settlements to be achieved. But as Fearon points out, grinding civil wars confound this story as “it strains credulity to imagine that the parties to a war that has been going on for many years … can hold any significant private information about capabilities or resolve.”[xxi] As a result, internal wars can end up frozen in place, and “parties can be locked in a completely unwinnable war despite the presence of mutually preferable deals.”[xxii]

  The second feature is the commitment problem that hinders the likelihood of stable, negotiated settlements in internal conflicts. Schmitt argues that one of the greatest achievements of early modern Europe was the capacity for wars between sovereign states to be “bracketed” by the resumption of peaceful coexistence.[xxiii] In other words, besides outright military victory, warring sovereign states can also choose to diplomatically terminate conflict and reestablish normal relations.[xxiv] The dynamics of intrastate wars, however, differ significantly; since both actors are struggling to occupy the same sovereign space, it is usually the case that one actor needs to be utterly extinguished for the conflict to end.[xxv] Fearon shows why this is such a significant problem for negotiated war termination in civil wars, namely that any outcome in which one actor ends up fully subordinated to the other begs for reneging and is hence unstable.[xxvi]

A third feature of internal wars is relevant for our analysis: making the war itself “profitable.” Fearon shows that this outcome is particularly likely to occur when both actors can make the civil war “pay” (usually through the exploitation of some appropriable rent-stream, such as drug trafficking or valuable natural resources).[xxvii] There is often a mutually reenforcing relationship between conflict and appropriable rent-streams as wealth can be generated as a flow of private goods that are easily controlled by force.[xxviii] The relevant aspect of this feature is that oftentimes the wealth associated with the rent-stream becomes highly valued by the conflict’s participants, in some cases arguably more so than the nominal goals of the actor.[xxix] Since these sources of rents are highly valued, threats to these streams provide a potential “lever” to shape actors’ behavior (a feature we exploit below).

Finally, rather than a bargaining problem among unitary actors, as is normally the case in inter-state war termination, the conflict may be more complicated. Since the conflict takes place within a non-functioning state, violence may be exercised by any number of players.[xxx] This may be due to the breakdown of command and control among factions or the proliferation of additional actors taking advantage of the opportunity to exploit the political vacuum created by war.[xxxi] In other words, events may occur within the conflict environment for which it is not clear who is responsible. This complexity makes bargaining processes significantly more difficult.[xxxii]

What does this body of work imply for asymmetric military interventions? If these four factors are pernicious features of intrastate conflict, why is our model not one of civil wars? The answer is that asymmetric interventions have an additional feature, one that is not common in civil wars. In asymmetric interventions, the conflict is an external and (often) trivial endeavor for one of the combatants.[xxxiii] Despite the asymmetric resource endowment, however, often the “powerful” intervenor fails to achieve victory; in fact, forty percent of asymmetric conflicts result in failure by the more powerful side.[xxxiv] If these well-resourced intervenors are unable to achieve “victory” through such costly activities as large-scale counterinsurgency (COIN) doctrine,[xxxv] what other strategies exist that might be sustained for lower costs? Answering this question is critical for American foreign policy, given the failures of the last two decades.

Our tacit collusive model provides a new strategic logic for stalemates by highlighting a mostly overlooked type of equilibrium that may exist within this class of conflicts. Beyond the three outcomes that have been the focus of the existing literature — (1) win/lose (one side militarily disarms the other), (2) draw (formally negotiated political settlement), or (3) continued fighting — we focus on a fourth: tacit collusion.[xxxvi] This equilibrium enables an outcome that is Pareto superior to continued fighting and would be a feasible outcome when victory or negotiated settlement are not attainable. It constitutes a relatively attractive form of coexistence within which both actors coordinate in refraining from overly injurious actions. In sum, a tacit collusive outcome is optimization within a stalemate.

Optimizing the Stalemate: Tacit Collusion

We now turn to an alternative way to conceive of strategies and outcomes in limited armed conflicts within the context of wider competition. To develop a useful model of such conflicts we need to diverge from the standard assumptions of a contest with a decisive culminating point and, instead, utilize a framework that allows for endless competitive interactions. Models of tacit collusion among firms provide an attractive set of tools for such an endeavor.

Our modeling choices diverge from the standard approach to formally modeling conflict: a Tulluck contest.[xxxvii] In such a contest, participants exert costly effort and victory is decided by a random variable with its distribution determined by the efforts of the participants. This framework presupposes that one actor in the conflict eventually “wins” (or at least the conflict is neatly settled).

In many recent and ongoing military conflicts, however, there is reason to believe that this framework is an ill fit. In asymmetric interventions, for example, the militarily powerful state may be too constrained by political considerations to bring their resources to bear, while the weaker side is simply incapable of destroying the forces of the invader; hence, a military resolution is rarely possible. Consequently, we have a very different operational environment than that described by a Tulluck contest. When stylized, the static equilibrium of a ‘stalemate game’ is essentially the outcome of a prisoners’ dilemma each period; costly battles—even when repeated over and over again—result in little real movement in territory. This setting shares key abstract features of price competition between rival suppliers in an industry in which neither firm will ever be able to eliminate the other. For this reason, we are able to utilize analytical tools from the literature on industry dynamics. Particularly, we show that in this setting there is a dynamic equilibrium that is better for both actors. In this equilibrium, each actor refrains from defection and is, further, incentivized to exert resources to prevent disruption by outside forces.

The idea that firms can use dynamic strategies to sustain supra-competitive profits is very old and based on the “folk theorem” in game theory. This idea was first formalized in a noncooperative repeated game setting by Friedman.[xxxviii] The literature on tacit collusion is now extensive and includes some powerful results.[xxxix] The basics of tacit collusion are as follows: Actors play a particular collusive path of strategies. In any given time period, there is a short-term benefit from defecting from the collusive path. The key to sustaining collusion is a punishment that is enacted if an actor defects from the collusive path. For a collusive path to be an equilibrium it must be that the short-term gain from defection is outweighed by the expected future punishment of taking such an action. Abreu established the idea that carrot and stick punishments paths can be optimal.[xl] This is a punishment that involves a brief hit of a “stick” and then returning to the collusive “carrot” path. Green and Porter and Abreu et al. expand this reasoning to a model of incomplete information and imperfect observability.[xli] In a setting when defections are not perfectly observable a carrot/stick form of collusion with periods of punishment (the stick) are on the equilibrium path. The finite periods of punishment are enacted after harm occurs to an actor and the actor cannot determine if the harm was intentional or not. These short-term punishments are essential to keep the players from taking actions that harm the other actor. The model we construct is built upon the results of this literature and includes periods of punishment on the equilibrium path.

Our choices build on previous work designed to model the interactions among terrorist groups and state actors.[xlii] This work seeks to reveal the dynamics that unfold between an irregular opponent that can leverage asymmetric informational advantages to inflict damage on a materially superior state.[xliii] Jacobson and Kaplan, for example model the exchange between targeted killings employed by the state versus suicide bombings employed by terrorists, focusing on the impact of relative patience between the two actors.[xliv] Bueno de Mesquita examines the tension between moderate and extremist factions common within terrorist groups and models the conditions under which the government may induce cooperation from moderate terror faction to aid in the contest with the extreme faction in infinitely repeated interactions.[xlv] More recent work, such as Baron, Berman, and Gavious, build on this work by analyzing empirical data of terror attacks and then building models to explain the observed patterns.[xlvi]

Such an approach has the novel implication of turning uncertainty on its head: Traditional military strategy emphasizes the need to “keep the enemy guessing” and maximize uncertainty, disruption, and surprise.[xlvii] This model, rather, seeks to find a stable equilibrium that is a mutually acceptable and sustainable outcome; players have a common understanding that unacceptable actions trigger swift, proportionate punishment while acceptable behavior goes unpunished. In the following section we provide a model of repeated conflict for a territorial space with the possible occurrence of unidentifiable acts of violence. We then characterize dynamic collusive strategies, and derive the conditions based on the model primitives for these strategies to be a mutually beneficial equilibrium.

A Model of an Unwinnable War

Consider two actors that are in a long-term conflict such that neither actor can hold territory without costly effort. The game takes place over discrete time periods , which go on indefinitely. Here we use the word “territory” to denote multidimensional span of control over the conflict environment. We use to denote an arbitrary actor and j is used to index the actor other than i. Actor i takes actions to fight for territory in time period that costs to the actor, where . Denote by , the vector of territorial fighting actions at time . The total value of holding control of the territory for each actor is . For simplicity we assume that regardless of the territorial distribution in the preceding period, it is just as difficult to hold or gain territory in the following period. Territorial distribution is determined for period t by military effort according to the function

where each is a continuously differentiable, bounded, concave and strictly increasing function from . Further, for . We allow a territorial split at the discontinuity point to be split such that , and for each actor .

The two actors can also take military actions that do not impact the territorial distribution but cause direct harm to the rival actor and create some positive effects for the actor taking the actions. We call these actions non-territorial military actions. For each actor , is used to denote non-territorial actions, with meaning the actions are taken and meaning they are not taken. Denote by , the vector of actions at time . The utility from taking these actions to actor is denoted by , with and . These action cause harm to the other actor specified by the function , with and . The last inequality imposes that the net benefit to both actors from the non-territorial military actions is negative.

There is also a positive probability that a non-territorial “terror” attack happens to actor by some rogue elements not following the instructions of actor . This type of attack occurs to actor with probability . This probability of an outside strike to actor can be reduced by the costly effort of actor . This is specified by , a continuously differentiable, concave and strictly decreasing function from . The effort level of actor is unobservable by the rival actor . This function captures the control each actor\ j has of their own forces as well as non-state actors in conflict environment. An environment with many rogue actors who are not controlled by actor involves a function that are larger at every effort level. We assume that the probability of an unauthorized terror strike hitting each actor is independent. A terror strike to actor causes that harm . There is no way for actor to know if the strike was a deliberate action of actor , or an action by some other external actor in the conflict environment.

Actor ‘s expected payoff of a particular time period is:

Each actor has a geometric discount factor . The expected payoff of actor at any time period is written

  Next, we consider equilibria of this repeated game.

All Out War

To begin the analysis, we focus on the equilibrium of the repeated game that does not involve dynamic strategies. This will be denoted as the War equilibrium and is composed of the repeated play of the static or one-shot Nash equilibrium from each period. Since the same one-shot game is repeated for each period , we are free to suppress the time subscript in our analysis. The additive separability of the payoff functions makes each player ‘s choices of each the variable , , and independent of each other. Let us begin by analyzing the static equilibrium choices of and , which are just basic optimization problems in which the optimal choice is not impacted by the other player ‘s choices. Player ‘s first order condition for effort is

and consequently, the equilibrium involves each player picking the minimal effort . The binary choice is also straightforward since gives an addition of utility , while the choice of results in zero added utility. Therefore, the optimal choice is .

Each period static game has the following unique one-shot Nash equilibrium in territorial actions that satisfy the following expression from the first order condition of each player :[xlix] For each , is implicitly defined by the expression

The one-shot Nash equilibrium expected payoff of player for any period is:

Each actor has a common geometric discount factor . Then actor ‘s discounted expected payoffs of the war equilibrium starting at any period can be written:

Dynamic Equilibrium: Tacit Collusion

In this section, we consider dynamic strategies that can improve the expected payoffs of both parties. The subgame perfect equilibrium that we focus on has the following character:

The equilibrium strategy involves each actor using the no war actions , and the territorial split is until a punishment is necessary. [l]

Each actor puts in effort to prevent outside actors attacking their rival defined by

For notational simplicity we write . Clearly, for both actors .[li]

The strategy we propose is based on each actor playing actions , each period until a defection from x or harm to an actor is observed. We label the actions of actor playing , from period onward is called the initial path of actor starting at period . The strategy we propose begins with each actor playing the initial path at time .

On this equilibrium path, there are two types of punishments triggered by two different events.

Punishment type 1: If either actor defects from at time , then a punishment is triggered. This action is perfectly observable so if the punishment path is sufficiently harsh, then it will never be observed on the equilibrium path. For simplicity we have each actor impose the punishment of forever (since it will never appear on the equilibrium path) non-collusive reversion for any such defection.

Punishment type 2: The second punishment type is triggered if an actor is harmed from a non-territorial attack. This punishment is triggered regardless of who caused the harm to actor . If the actor is on the actor ‘s initial path at time and actor receives harm at time , then actor switches to single period of punishment at time . The punishment is to play for period . As long as there is no harm to actor at period , actor plays ‘s initial path from onward.

Notice that during a period of actor punishment by playing , actor is still on ‘s initial path. Thus, if harm is inflicted to actor in this period, then another period of punishment by actor will follow.

The single period expected payoff of these actions for actor is

Given the implementation of this by both actors within the dynamic strategy with regards to actions x and a, each actor maximizes her own discounted expected payoff by picking . This is an important feature of these dynamic strategies: each actor puts in effort to stop terror attacks on the other actor , because they internalize some of the cost of the terror attack to their rival via an increased probability of the punishment type 1. The incentive to minimize terror attacks to your rival is a distinct feature of this dynamic strategy.

The statement of the following proposition includes the conditions such that this dynamic strategy is a subgame perfect equilibrium.

Proposition 1 The dynamic strategy is a subgame perfect equilibrium if for both actors ,

The inequality in the proposition highlights that the key to these strategies being a subgame perfect equilibrium is that each actor must be sufficiently patient. That is, the value of utility tomorrow compared to today must be high enough that a defection today is not worth the punishment tomorrow for either actor. This must be true for both types of defections. First, the gain to an actor from terror type attacks is outweighed by the punishment of a retaliatory attack next period. Second, the short-term gains from fighting for territory are outweighed by resulting punishment of battles in the future. Given these dynamic strategies are a subgame perfect equilibrium, the equilibrium effort to mitigate terrorism on the other actor is an optimal choice for actor at each time period . This effort weighs the cost of effort against the decreased probability of being punished by the other actor next period for a terror attack that came from a rogue element.

Conclusion: Rethinking Afghanistan

The model presented here provides general prescriptions for an entire class of conflicts: limited armed conflicts where neither actor is capable of defeating the other. By moving beyond the assumptions built into the Tulluck contest and borrowing the architecture of tacit collusion among oligopolistic firms, we have identified optimal strategies for an entire class of conflicts that have befuddled military planners in recent decades. As such, we contribute to a growing literature that leverages insights from the folk theorem for better understanding armed conflict. Our model suggests that conceiving of strategy in such conflicts as tacit collusive equilibria would not lead to “victory” but would rather achieve valued results at much lower cost.

We began this article with reference to Afghanistan. How could this conflict have been approached differently once the war sank into stalemate? We explore this question with some counterfactual reasoning here.

First, it is easy to establish that altering the territorial division of the conflict for either side became cost prohibitive as the conflict dragged on.[lii] By the last few years of the war United States forces were limited to operating within “med rings” (rings determined by the ability to transport wounded soldiers to surgery facilities within one “golden” hour).[liii] This had been true since the cessation of direct American combat operations and the failure of the “Village Stability Operations” campaign (2009-2014) to contest Taliban control in the hinterlands of Afghanistan.[liv] Conversely, it was also exceedingly difficult for the Taliban to have made significant gains within these rings and they rarely sought to do so. Once the territorial fighting effectively stopped, the essential conditions of the tacit collusion equilibrium were set and understood by both sides. This is an important component of the tacit collusive strategies we are exploring, that actors come to recognize the futility of spending additional resources to change the territorial distribution within the context of an “unwinnable” war.

The second component of the model concerns the capacity for each actor to inflict punishments on the other that are not designed to contest the territorial division – what we have labeled as “terror attacks.” The model speaks to the conditions under which these “terror attacks” form part of the collusive strategy, particularly when there may be attribution concerns around terror strikes from “rogue” elements within a confusing operational environment. In the case of Afghanistan, the Taliban had the capacity to conduct terror attacks within the urban areas.[lv] Less well known, however, was the American capacity to inflict non-territorial punishment on the Taliban. Rather than inflicting additional casualties on the Taliban forces (they were largely insensitive to such killing and were regularly able to turn such strikes to their advantage through propaganda) the “terror strike” tool available to American forces was the painful disruption of the Taliban’s heroin industry through the targeted bombing of the presses which processed opium into heroin. Over the course of the war, the Taliban had grown into the world’s largest exporter of heroin[lvi] and disrupting the processing of their heroin production provided an exceedingly attractive lever to be pulled by U.S. forces. Bombing the heroin refining locations cut into the Taliban’s profits; it also generated friction between the Taliban cartel and the rural Afghan poppy farmers upon whom they relied for political support and the supply of opium.[lvii] To be clear, disrupting heroin production in the context of our proposed strategy would not be intended to cripple or eradicate the heroin trade,[lviii] but would rather be used sparingly and instrumentally to maintain tacit collusion.

Building on the stability of territorial distribution, the strategic use of such “terror” strikes by both sides could have allowed both actors to develop a tacit collusive relationship that identified a mutually acceptable state of affairs within Afghanistan, as well as low-cost tools to maintain that outcome in an endogenously binding equilibrium. This could have set the stage for an even more attractive form of mutually beneficial cooperation concerning rogue elements within the operational environment. Consider that the original purpose of the American invasion of Afghanistan was ending Taliban support for trans-national terrorism. The Taliban seemed to have never been terribly interested in global Jihad and had shown itself to be quite uncomfortable with ISIS militants operating in the Eastern regions of the country.[lix] The model presented here serves to exploit such antipathy through discrete punishments. It prescribes strategic actions in light of information asymmetries regarding the attribution of terrorist attacks and amplifies existing shared interest in “policing” such trans-national terrorist groups that operated in Afghanistan.[lx] If fully realized, the framework presented here illuminated a path towards achieving this central goal of the 2001 invasion – the prevention of Afghanistan reemerging as a base for transnational terrorism – at a fraction of the cost of a counterinsurgency campaign.

The greatest challenge to implementing the strategic concepts posited here is the political appetite to sustain a military conflict — even a minimally costly one — for an indefinite period of time within the domestic American arena. The political pressure around military commitments tends to vary with the size of the forces deployed, with the deployment of large, conventional forces significantly increasing the “flow of sand through the political hour-glass.”[lxi] Given this constraint, U.S. SOF forces have the capacity to deploy small numbers of troops while retaining the ability to plan and execute sensitive and strategic operations in semi-permissive or non-permissive environments. Therefore, U.S. SOF units seem best suited to operationalize the concepts outlined here in a manner that might sustain political will.

To summarize the application to Afghanistan, the model presented here would not have offered a path to military “victory” in Afghanistan. It rather would have provided fresh strategic thought for the small footprint of forces that the Chairman of the Joint Chiefs and the Central Command’s Commanding General claim to have advocated to President Biden in the wake of the controversial withdrawal from Afghanistan.[lxii] It does so by providing a logical basis for cheaply sustaining armed conflicts to achieve limited aims; this is particularly attractive in the context of managing wider competition and resource constraints for an indefinite period. Further, if one assumes that the United States will face similar militarized conflicts in the future—and based on the record of American interventions since the Second World War, this is a safe bet[lxiii]—then the model presented here provides a novel strategy for cheaply managing them. In an oncoming era in which both fiscal constraints and the rise of peer competitors may make “winning” strategies prohibitively expensive, the “management” strategies presented here will become more attractive. Finally, we suspect that the logic offered here can scale to other domains of strategic competitions that last for indefinite periods and in which all out conflict is prohibitively costly and the likelihood of ultimate victory is very small or absent. Future work will explore such extensions of the model.

Appendix: Proof of Proposition 1

We now show that this inequality is sufficient to guarantee that neither actor will defect from the dynamic strategy outlined in Proposition 1. The proof is done by verifying these dynamic strategies are in fact a subgame perfect equilibrium for any discount factors weakly larger than the bound in the statement of the proposition.

We begin by showing that, given is played in each period, choosing each period is supported by the dynamic strategy.

First, we denote by actor ‘s discounted expected payoff of the stable peace strategy starting at any period . At an arbitrary time period the stable peace has expected payoff for period , since with probability actor was harmed last period. Thus, we can write for

and

=

Now we consider the case that actor defect from her initial path. This defection can only occur if last period no harm was inflicted on actor . The single period defection profit minus collusive profit is . The future loss from this defection is the harm of for sure next period instead of the expected harm of . The incentive compatibility constraint for not defecting to is

Rewritten in terms of a bound on the discount factor we have,

Second, we consider defections from . Given such a defection at time , the actors switch to the static Nash equilibrium from onward. The upper bound of the gain from defection for either actor happens at the limit of as . The incentive compatibility constraint for collusion must cover all , which means it must cover the upper bound . The incentive compatibility constraint for actor non-territorial action in all periods is:

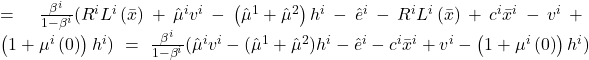Rewritten in terms of the discount factor we have,

For time period 1, this constraint is slightly different

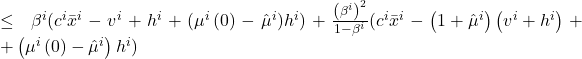
Rewritten in terms of the discount factor, we have

The discount factor bound for period 1 is larger than in any period and is the bound used in the statement of the proposition.

Finally, we verify that each actor picking at every time is an equilibrium. We write the discounted expected payoff for player from time onward given the dynamic equilibrium by both players for all , except any effort can be picked in period .

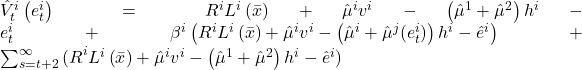
Then maximizing with respect to we attain the first order condition

The unique solution to this problem is .

Endnotes

---

[i] This research grew from the direct experience of two of the authors who analyzed these issues on the ground in Afghanistan during the Fall of 2016.

[ii] Rebecca Shabad, “Contradicting Biden, top generals say they recommended a small force stay in Afghanistan,” NBC News, 28 September 2021, https://www.nbcnews.com/politics/congress/pentagon-leaders-austin-milley-face-questions-chaotic-afghanistan-withdrawal-n1280230.

[iii] Joint Chiefs of Staff, Joint Concept for Competing (Washington, D.C.: Joint Chiefs of Staff, 2022), iii.

[iv] Ali Wyne, “In Afghanistan, A Protracted Stalemate,” The RAND Blog, 26 February 2018, https://www.rand.org/blog/2018/02/in-afghanistan-a-protracted-stalemate.html; Christopher D. Kolenda, “Slow Failure: Understanding America’s Quagmire in Afghanistan,” Journal of Strategic Studies 42:7 (2019): 992-1014.

[v] Ellen Mitchell, “Afghanistan War at a Stalemate, Top General Tells Lawmakers,” The Hill, 4 December 2018, https://thehill.com/policy/defense/419739-afghanistan-war-at-a-stalemate-top-general-tells-lawmakers.

[vi] James M. Lindsay, “Campaign Foreign Policy Roundup: What to Do About Afghanistan?” Council on Foreign Relations: The Water’s Edge Blog, 16October 2020, https://www.cfr.org/blog/campaign-foreign-policy-roundup-what-do-about-afghanistan.

[vii] Reuters, “Trump Pledges to Withdraw Troops from Afghanistan by Christmas; Taliban Cheer,” NBC News, 8 October 2020, https://www.nbcnews.com/news/world/trump-pledges-withdraw-troops-afghanistan-christmas-taliban-cheer-n124259.

[viii] Joshua Keating, “The Forever War Won’t End Until Congress Ends It,” Slate, 5 May 2021, https://slate.com/news-and-politics/2021/05/biden-afghanistan-aumf-forever-war-power-congress.html.

[ix] Ali Wyne, “The Risks of Permanent War,” The RAND Blog, 28 September 2018, https://www.rand.org/blog/2018/09/the-risks-of-permanent-war.html.

[x] Carl von Clausewitz, On War, trans. M.E. Howard and P. Paret (Princeton: Princeton University Press, 1989), 91.

[xi] This prescriptive application of our model accords with Aumann’s insights on game theory that “the distinction between the descriptive and the normative modes is not as sharp as might appear… solution concepts will often have both descriptive and normative interpretations.” Robert Aumann, “What is Game Theory Trying to Accomplish?” in Frontiers of Economics, ed.K. Arrow and S. Honkapohja (Oxford: Basil Blackwell, 1985), 13.

[xii] We follow the usage of the term internal war as Eckstein: “The term ‘internal war’ denotes any resort to violence within a political order to change its constitution, rulers, or policies … Nor does it mean quite the same thing as certain more commonly used terms, such as revolution, civil war, revolt, rebellion, uprising, guerrilla warfare, mutiny, jacquerie, coup d’etat, terrorism, or insurrection. It stands for the genus of which the others are species.” Harry Eckstein, “On the Etiology of Internal Wars,” History and Theory, 4:2 (1965): 133-163, 113.

[xiii] Dan Reiter, How Wars End (Princeton: Princeton University Press 2009), 1.

[xiv] Paul Kecskemeti, Strategic Surrender: The Politics of Victory and Defeat (Stanford: Stanford University Press, 1958); Fred Charles Ikle, Every War Must End (New York: Columbia University Press, 1971).

[xv] Allan C. Stam, Win, Lose, or Draw: Domestic Politics and the Crucible of War (Ann Arbor: University of Michigan Press, 1996); H.E. Goemans, War and Punishment: The Causes of War Termination and the First World War (Princeton: Princeton University Press, 2000); Reiter, How Wars End; Donald Wittman, “How a War Ends: A Rational Model Approach,” Journal of Conflict Resolution, 23:4, (1979): 743-763; Paul Pillar, Negotiating Peace: War Termination as a Bargaining Process (Princeton: Princeton University Press, 1983).

[xvi] Clausewitz, On War, 69; R. Harrison Wagner, “Bargaining and War,” American Journal of Political Science 44:3 (2000): 469-484.

[xvii] Stam, Win, Lose, or Draw, 35.

[xviii] R. Harrison Wagner, War and the State: The Theory of International Politics (Ann Arbor: University of Michigan Press, 2007), 150.

[xix] Wagner, War and the State, 153.

[xx] Robert Powell, “Bargaining and Learning While Fighting,” American Journal of Political Science, 48:2 (2004): 344-361; Branislav Slantchev, “The Principle of Convergence in Wartime Negotiations,” American Political Science Review, 97:4 (2003): 621-632.

[xxi] James D. Fearon, “Why do Some Civil Wars Last So Much Longer than Others?” Journal of Peace Research, 41:3 (2004): 275-301, 290.

[xxii] Fearon, “Why Do Some Civil Wars,” 294; see also Jean-Pierre Langlois and Catherine C. Langlois, “Does the Principle of Convergence Really Hold? War, Uncertainty, and the Failure of Bargaining,” British Journal of Political Science, 42:3 (2011): 511-536.

[xxiii] Carl Schmitt, The Nomos of the Earth in the International Law of Jus Publicum Europaeum (Candor, NY: Telos Press, 2006).

[xxiv] Louiza Odysseos and Fabio Petito, “Introduction,” in The International Political Thought of Carl Schmitt: Liberal War, and the Crisis of Global Order, ed.L. Odysseos and F. Petito (London: Routledge, 2007).

[xxv] Gordon H. McCormick, Steven B. Horton, and Lauren A. Harrison, “Things Fall Apart: The Endgame Dynamics of Internal Wars,” Third World Quarterly, 28:2 (2007): 321-367.

[xxvi] Fearon, “Why Do Some Civil Wars”; Barbara F. Walter, “Bargaining Failures and Civil War,” Annual Review of Political Science, 12 (2009): 243-261.

[xxvii] Fearon, “Why Do Some Civil Wars,” 294.

[xxviii] Jeffrey Frieden, “International Investment and Colonial Control: A New Interpretation,” International Organization, 48:4 (1994): 559-593; Kevin M. Murphy, Andrei Shleifer, and Robert W. Vishny, “Why is Rent-Seeking So Costly to Growth?” American Economic Review, 83:2 (1993): 409-41.

[xxix] Michael Ross, “A Closer Look at Oil, Diamonds, and Civil War,” Annual Review of Political Science, 9 (2006): 265-300.

[xxx] Peter Rudloff and Michael G. Findlay, 2016. “The Downstream Effects of Combatant Fragmentation on Civil War Recurrence,” Journal of Peace Research, 53:1 (2016): 19-32.

[xxxi] Michael Burch and Leslie Ochreiter, “The Emergence of Splinter Factions in Intrastate Conflict,” Dynamics of Asymmetric Conflict, 13:1 (2019): 47-66; Mohammed M. Hafez, “Fratricidal Rebels: Ideological Extremity and Warring Factionalism in Civil Wars,” Terrorism and Political Violence, 32:3 (2020): 604-629.

[xxxii] Gordon H. McCormick and Guillermo Owen, “Factionalism, Violence and Bargaining in Civil Wars,” Homo Oeconomicus XX:4 (2004): 361-390.

[xxxiii] Ariel E. Levite, Bruce W. Jentleson, and Larry Berman, eds, Foreign Military Intervention: The Dynamics of Protracted Conflict (New York: Columbia University Press, 1994); Gil Merom, How Democracies Lose Small Wars (New York: Cambridge University Press, 2003).

[xxxiv] Patricia Sullivan, Who Wins? Predicting Strategic Success and Failure in Armed Conflict (New York: Oxford University Press, 2012), 4; see also Andrew Mack, “Why Big Nations Lose Small Wars: The Politics of Asymmetric Conflict,” World Politics, 27:2 (1975): 175-200; Ivan Arreguin-Toft, “How the Weak Win Wars: A Theory of Asymmetric Conflict,” International Security, 26:1 (2001): 93-128.

[xxxv] David Kilcullen, Counterinsurgency (New York: Oxford University Press, 2010).

[xxxvi] Although repeated prisoner’s dilemma games, which focus on dynamic equilibrium that qualify as “tacit collusion,” have been used to understand international conflict since Shubik, dynamic strategies using these insights have remained on the sidelines with regards guiding strategy in asymmetric conflicts. See Marin Shubik, “Game Theory, Behavior, and the Paradox of the Prisoner’s Dilemma: Three Solutions,” Journal of Conflict Resolution, 14:2 (1970): 181-193.

[xxxvii] For a review of this literature see Erik O. Kimbrough, Kevin Laughren, and Roman Sheremeta, “War and Conflict in Economics: Theories, Applications, and Recent Trends,” Journal of Economic Behavior & Organization, 178 (2017): 998-1013.

[xxxviii] James Friedman, “A Non-cooperative Equilibrium for Supergames,” Review of Economic Studies, 38:1 (1971): 1-12.

[xxxix] Feuerstein provides an excellent survey of the theoretical literature on tacit collusion. Switgard Feuerstein, “Collusion in Industrial Economics: A Survey,” Journal of Industry, Competition and Trade, 5 (2005): 163-198.

[xl] Dilip Abreu, “Extremal Equilibria of Oligopolistic Supergames,” Journal of Economic Theory, 39:1 (1986): 191-225; Dilip Abreu, “On the Theory of Infinitely Repeated Games with Discounting,” Econometrica, 56:2 (1988): 383-396.

[xli] Edward H. Green and Robert J. Porter, “Noncooperative Collusion under Imperfect Price Information,” Econometrica, 52:1 (1984): 87-100; Dilip Abreu, David Pearce, and Ennio Stacchetti, “Optimal Cartel Equilibria with Imperfect Monitoring,” Journal of Economic Theory, 39:1 (1986): 251-269; Dilip Abreu, David Pearce, and Ennio Stacchetti, “Toward a Theory of Discounted Repeated Games with Imperfect Monitoring,” Econometrica, 58:5 (1990): 1041-1063.

[xlii] For surveys of this work see Todd M. Sandler and Kevin Siqueira, “Global terrorism: Deterrence versus pre-emption,” Canadian Journal of Economics, 39:4 (2006): 1370-1387; Walter Enders and Todd Sandler, The Political Economy of Terrorism (New York: Cambridge University Press, 2012).

[xliii] B.J. Brophy-Baermann and A. C. Conybear, “Retaliating against terrorism: Rational Expectations and the Optimality of Rules versus Discretion,” American Journal of Political Science 38:1 (1994): 196-210.

[xliv] D. Jacobson and E. H. Kaplan, “Suicide Bombings and Targeted Killings in (Counter-) Terror Games,” Journal of Conflict Resolution, 51:5 (2007): 772–792.

[xlv] Ethan B. Bueno De Mesquita, “Conciliation, counterterrorism, and patterns of terrorist violence,” International Organization, 59:Winter (2005): 145-176.

[xlvi] Opher Baron, Oded Berman, and Arieh Gavious, “Game Between a Terrorist and a Defender,” Production and Operations Management, 27:3 (2017): 433-457. In two other closely related papers, Acemoglu and Wolitzky and Yared, use repeated games with imperfect observability to provide new understanding on the nature of international conflict. Acemoglu and Wolitzky provide an “overlapping generations” model conflict spirals in which agents eventually learn that the conflict began based on a misperception and switch back to good actions, thereby restarting the cycle. Daron Acemoglu and Alexander Wolitzky, “Cycles of Conflict: An Economic Model.” American Economic Review, 104:4 (2014): 1350-1367. Yared provides a model of conflict with an aggressive and non-aggressive county in which the efficient outcome can only be sustained by equilibrium strategies that involve temporary wars. Pierre Yared, “A Dynamic Theory of War and Peace,” Journal of Economic Theory, 145 (2010): 1921-1950.

[xlvii] For a critical analysis on this topic, see Leo J. Blanken, “Reconciling Strategic Studies… with Itself: A Common Framework for Choosing Among Strategies,” Defense and Security Analysis 28:4 (2012): 275-287.

[xlviii] We use the term “terror” in spite of the fact that these strikes do not necessarily fit the formal definition of terrorism. The accepted definition of terrorism from Enders and Sandler is “the premeditated use, or threat of use, of extra-normal violence or brutality to obtain political objective through intimidation or fear directed at a large audience.” We do not specify the purpose of the attacks or that they involve extra-normal violence. The term is only used informally because what we call terror attacks includes the case of terrorism. Walter Enders and Todd Sandler, “Terrorism: Theory and Applications,” in Handbook of Defense Economics, Volume 1, ed. K. Hartley and T. Sandler (New York: North-Holland, 1995), 213.

[xlix] Uniqueness of equilibrium follows from Proposition 1 of Takashi Yamazaki, “On the Existence and Uniqueness of Pure-Strategy Nash Equilibrium in Asymmetric Rent-Seeking Contests,” Journal of Public Economic Theory, 10:2 (2008): 317-327.

[l] Although the territorial split or “sharing rule” at  can be an endogenous part of the dynamic equilibrium we fixed it at the split of . The intuition for this procedure is that we are assuming the two actors retain the existing distribution of territory when foregoing “all out” conflict. Conditions for similar dynamic equilibrium to the one we outline can be constructed for a range of similar territorial distributions.

[li] Note the  is simply the solution to each actor ‘s discounted expected utility maximization problem given the dynamic strategies outlined below.

[lii] Anthony H. Cordesman, “The State of the Fighting in the Afghan War in Mid-2019,” Center for Strategic and International Studies, 2019, https://www.csis.org/analysis/state-fighting-afghan-war-mid-2019

[liii] Ben Barry, “Battlefield Medicine: Improving Survival Rates and the ‘Golden Hour’,” International Institute of Strategic Studies, 2019, https://www.iiss.org/blogs/military-balance/2019/04/battlefield-medicine

[liv] William Knarr and Mark Nutsch, Village Stability Operations and the Evolution of SOF Command and Control in Afghanistan: Implications for the Future of Irregular Warfare (MacDill AFB: Joint Special Operations University Press, 2020).

[lv] Andrew Wilder, “What’s Behind the Spike in Deadly Terror Attacks in Afghanistan?” United Institute of Peace,2018, https://www.usip.org/publications/2018/01/whats-behind-spike-deadly-terror-attacks-afghanistan.

[lvi] Alfred W. McCoy, “How the Heroin Trade Explains the US-UK Failure in Afghanistan.” The Guardian, 9January 2018, https://www.theguardian.com/news/2018/jan/09/how-the-heroin-trade-explains-the-us-uk-failure-in-afghanistan

[lvii] Dan Lamothe, “The US begins bombing Taliban drug labs as Trump’s Afghanistan strategy takes hold,” Washington Post, 20 November 2017, https://www.washingtonpost.com/news/checkpoint/wp/2017/11/20/the-u-s-begins-bombing-taliban-drug-labs-as-trumps-afghanistan-strategy-takes-hold/?utm_term=.c8831b8efa66

[lviii] David Mansfield, “Bombing Heroin Labs in Afghanistan: The Latest Act in the Theater of Counternarcotics.” London School of Economics Drug Policy Unit, 2018, https://www.lse.ac.uk/united-states/Assets/Documents/Heroin-Labs-in-Afghanistan-Mansfield.pdf

[lix] Wesley Morgan, “Our Secret Taliban Air Force: Inside the Clandestine US Campaign to Help Our Longtime Enemy Defeat ISIS,” Washington Post, 22 October 2020, https://www.washingtonpost.com/outlook/2020/10/22/taliban-isis-drones-afghanistan/?arc404=true

[lx] Shawn Snow, “ISIS Loses More than Half of Its Fighters from US Airstrikes and Taliban Ground Operations,” Military Times, 27 February 2020, https://www.militarytimes.com/flashpoints/2020/02/27/isis-loses-more-than-half-its-fighters-from-us-airstrikes-and-taliban-ground-operations/

[lxi] John Bleigh, Justin Hufnagel, and Curt Snider, “Institutional Challenges to Developing Metrics of Success in Irregular Warfare” (master’s thesis, Defense Analysis Department, Naval Postgraduate School, 2011).

[lxii] Leo Blanken and Stephen Rodriguez, “The Strategic Logic of a Forever War,” Foreign Policy, 8 September 2021, https://foreignpolicy.com/2021/09/08/afghanistan-biden-sunk-costs-forever-war/

[lxiii] Barbara Salazar Torreon and Sofia Plagakis, Instances of Use of United States Armed Forces Abroad, 1798-2022 (Washington D.C.: Congressional Research Service, 2022).